Background
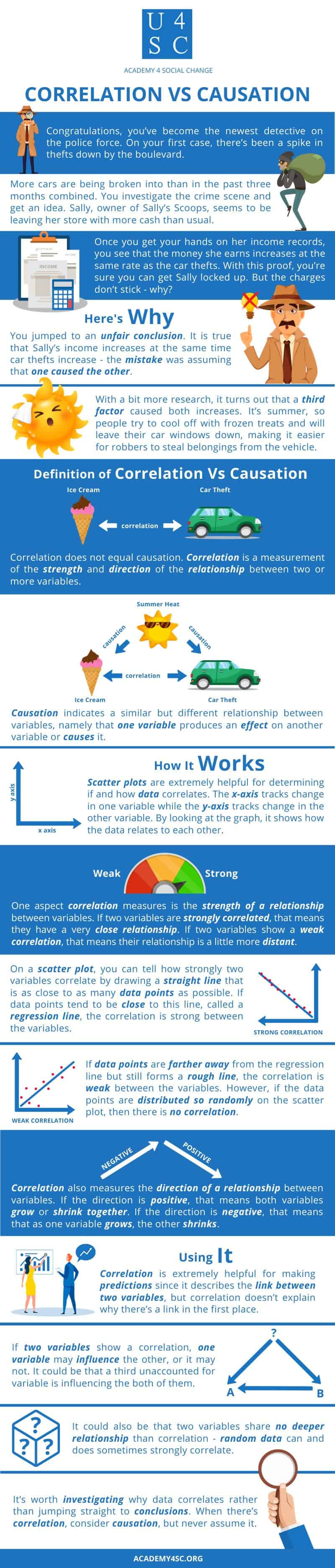
Congratulations, you’ve become the newest detective on the police force. It’s a bright summer day when you get your first case. There’s been a spike in thefts down by the boulevard. More cars are being broken into than in the past three months combined. You investigate the crime scene and get an idea. Sally, owner of Sally’s Scoops, seems to be leaving her store with more cash than usual. Once you get your hands on her income records, you see that the money she earns increases at the same rate as the frequency of car thefts. With this proof, you’re sure you can get Sally locked up for good. But the charges don’t stick - why?
Here’s Why
You jumped to an unfair conclusion. It is true that Sally’s income increases at the same time car thefts increase - the mistake was assuming that one caused the other. With a bit more research, it turns out that a third factor, one you had neglected to consider, caused both increases. It’s summer, so it’s hot - people try to cool off with frozen treats and will leave their car windows down, making it easier for robbers to steal belongings from the vehicle.
Correlation vs Causation
Correlation does not equal causation. Correlation is a measurement of the strength and direction of the relationship between two or more variables. Causation indicates a similar but different relationship between variables, namely that one variable produces an effect on another variable or causes it.
How It Works
Scatter plots are extremely helpful for determining if and how data correlates. The x-axis tracks change in one variable while the y-axis tracks change in the other variable. By looking at the graph, it’s easy to track changes in both variables, putting a focus on how the data relates to each other.
Data can correlate in five basic ways. Two variables can be strongly or weakly correlated and they can be positively or negatively correlated too. Of course, two variables can show no correlation, which means they don’t share a relationship at all.
One aspect correlation measures is the strength of a relationship between variables. “Strong” and “weak” are describing that relationship. Therefore, if two variables are strongly correlated, that means they have a very close relationship - like the relationship between Sally’s income and the number of thefts at the street by the beach. If you knew how much money Sally took home on Tuesday, you’d probably come up with a very close guess to how many thefts occurred that day, too. Meanwhile, if two variables show a weak correlation, that means their relationship is a little more distant. The number of kitchen knives sold per year and the number of violent crimes per year may weakly correlate, for example. Some people may buy the knives as a weapon, but most of us are just trying to cut up vegetables, so a giant spike in knife sales one year might show no change in violent crime rates.
On a scatter plot, you can tell how strongly two variables correlate by drawing a straight line that is as close to as many data points as possible. If data points tend to be close to this line, called a regression line, the correlation is strong between the variables. If data points are farther away from the regression line but still forms a rough line, the correlation is weak between the variables. However, if the data points are distributed so randomly on the scatterplot that it is impossible to draw a neat regression line, then there is no correlation.
Correlation also measures the direction of a relationship between variables. If the direction is positive, that means both variables grow or shrink together. For example, the number of cigarettes a person smokes weekly positively correlates with their overall score on an anxiety test. That means that a low anxiety score is associated with a low use of cigarettes while a high anxiety score is associated with a high use of cigarettes. Two variables can also negatively correlate, like the number of absences a student has and their SAT score. This means that as one variable grows, the other shrinks. For example, if a student has a high number of absences, they’re likely to have a low SAT score. If they have a low number of absences, they’re more likely to have a high SAT score.
Using It
Correlation is extremely helpful for making predictions since it describes the link between two variables, but correlation doesn’t explain why there’s a link in the first place. If two variables show a correlation, one variable may influence the other, or it may not. It could be that a third unaccounted for variable is influencing the both of them, like how the weather caused a spike in both ice cream profits and car thefts in the opening example. It could also be that two variables share no deeper relationship than correlation - random data can and does sometimes strongly correlate.
Proving that one variable causes a change in another is a much more involved process. In essence, three main conditions must be met. Firstly, when one variable changes, the other must change in tandem. Graphing a scatter plot of the data and finding if and how the variables correlate will give you a good headstart on this step. From there, you can see if the variables really do change together. Secondly, time order must be established. One variable has to occur before a change is noticed in the second variable, i.e. the cause must come before the effect. This step directly follows into the third and final step: eliminate alternative explanations and third variables. If you want to prove that Sally is the car burglar, you have to verify that her income increases after cars are broken into, that her ice cream sales haven’t gone up, and that the fact that it’s summer has no bearing on the situation. Showing correlation isn’t even a full step to proving causation.
It’s worth investigating why data correlates rather than jumping straight to conclusions. When there’s correlation, consider causation, but never assume it.